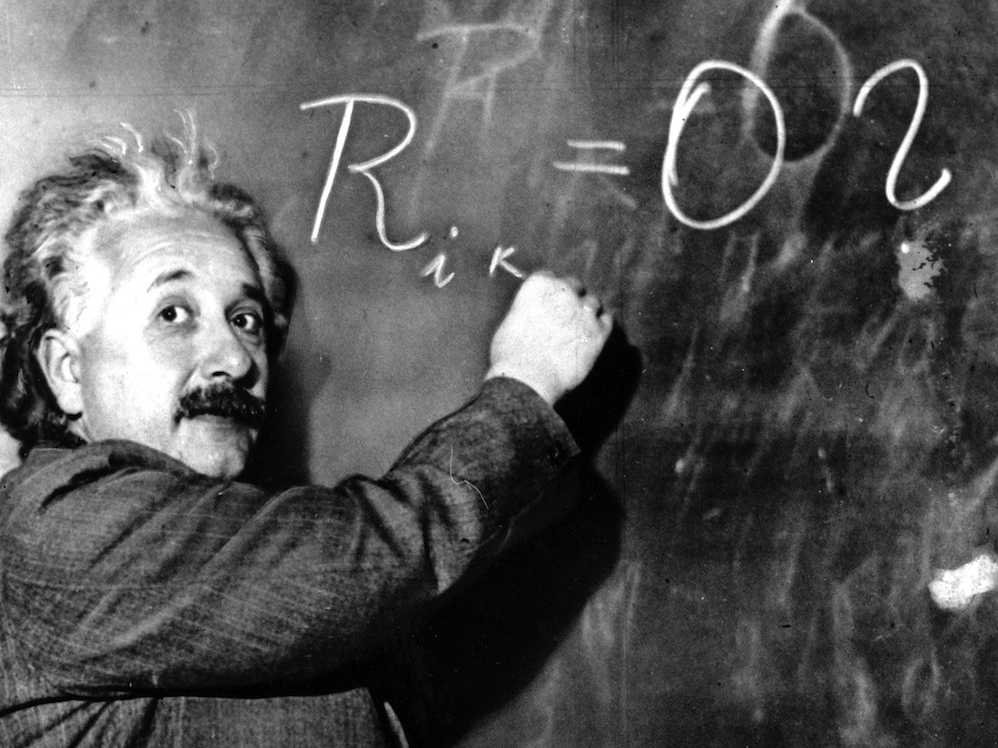Ας δούμε ποιοι είναι οι πιο έξυπνοι άνθρωποι όλων τον εποχών στον κόσμο
40. Richard “Rick” Rosner
Η τηλεοπτική περσόνα και πρώην στρίπερ Ρικ Ρόσνερ, είναι ένας από τους πιο έξυπνους εν ζωή άντρες στον κόσμο με IQ που κυμαίνεται από 140 μέχρι 250, ανάλογα τις διαφορετικές μετρήσεις. Έχει κάνει πάνω από 30 διαφορετικά IQ τεστ και είχε πολύ υψηλό σκορ σε πάνω από 20.
39. Marilyn vos Savant
Γεννημένη το 1946, η Βος Σάβαντ έχει IQ από 157 έως 228. Εγκατέλειψε το πανεπιστήμιο μετά τα δύο χρόνια και ασχολήθηκε με τα μεσιτικά. Έγινε διάσημη το 1985 όταν σκόραρε 228 στο IQ τεστ και μπήκε στο βιβλίο Ρεκόρ Γκίνες της χρονιάς εκείνης.
38. Christopher Langan
Με IQ ανάμεσα στο 174 και 210, ο Λανγκάν έχει χαρακτηριστεί από το περιοδικό Esquire ως ο πιο έξυπνος άντρας στην Αμερική. Σηκώνει βάρη, ήταν αγοραφοβικός και πληρώνει τους λογαριασμούς του κάνοντας προσωρινές δουλειές ως μπάρμαν, «πόρτα» σε νυχτερινά μαγαζιά και γυμναστής.
37. Nathan Leopold
Γεννημένος στο Σικάγο το 1904, ο Λέοπολντ ήταν παιδί θαύμα με IQ 210 και είπε την πρώτη του λέξη σε ηλικία 4 μηνών. Επιπλέον, ήταν και δολοφόνος, αφού με τον φίλο του σκότωσαν ένα 14χρονο αγόρι στην προσπάθειά τους να κάνουν το τέλειο έγκλημα.
36. Marnen Laibow-Koser
Αφού αρίστευσε στα IQ τεστ που έκανε στην παιδική του ηλικία, προέβλεψαν ότι το IQ του θα είναι 268. Σήμερα είναι ένας 39χρονος συνθέτης και προγραμματιστής που φτιάχνει εφαρμογές για το διαδίκτυο και μένει στη Μασαχουσέτη.
35. Ainan Cawley
Ο Ainan Cawley είναι μόλις 14 χρονών. Τα IQ τεστ του είναι ανάμεσα στο 263-349, σύμφωνα με διάφορες μετρήσεις. Ζει στη Σιγκαπούρη, όπου δίνει επιστημονικές διαλέξεις από την ηλικία των 6 ετών και στα 8 του χρόνια γράφτηκε στο Πολυτεχνείο της Σιγκαπούρης.
34. Adragon De Mello
Αποφοίτησε από το πανεπιστήμιο σε ηλικία 11 ετών και έχει IQ 400. Για το μυαλό του έχει να ευχαριστεί τον πατέρα του, ο οποίος πίστευε τόσο πολύ ότι ο γιος του θα κερδίσει βραβείο Νόμπελ μέχρι να γίνει 16 χρονών που τον πίεσε πολύ για να πετύχει.
33. Michael Kearney
Γεννημένος στην Χαβάι το 1983, ο Kearney πήρε το πτυχίο του από το Πανεπιστήμιο της Ν. Αλαμπάμα σε ηλικία 10 ετών. Το IQ του εκτιμάται ότι είναι ανάμεσα στο 200 και το 325 και όταν ήταν μικρός διαγνώστηκε από Διαταραχή Ελλειμματικής Προσοχής- Υπερικινητικότητα (ΔΕΠ-Υ). Μέχρι τα 22 του χρόνια είχε καταφέρει να πάρει 4 πτυχία και να κάνει διδακτορικό στην Χημεία.
32. Nadia Camukova
Έχει IQ 200 και γεννήθηκε στη Μόσχα το 1976. Μιλάει επτά γλώσσες και γνωρίζει οκτώ τούρκικες διαλέκτους και είναι καθηγήτρια στο Πανεπιστήμιο Bahçeşehir στην Τουρκία.
31. Michael Grost
Ο Michael Grost έχει IQ 200 και ήταν μόλις 10 ετών όταν άρχισε τις σπουδές του στο Πανεπιστήμιο του Μίσιγκαν το 1964. Αργότερα, σπούδασε στο Γέιλ και από το 2005 δουλεύει σε μία εταιρεία υπολογιστών στο Ντιτρόιτ. Τα ενδιαφέροντά του είναι η ζωγραφική και η εξελικτική βιολογία.
30. Sho Yano
Μπήκε στο Πανεπιστήμιο όταν ήταν μόλις 9 ετών και έχει IQ 200. Σπούδασε ιατρική από τα 12 μέχρι τα 21 του χρόνια και έγινε ο νεότερος άνθρωπος που πήρε πτυχίο ιατρικής.
29. Dylan Jones
Ο Jones που έχει IQ 200, αποφοίτησε στα 16 από το πανεπιστήμιο του Κολοράντο που πήρε πτυχίο στα μαθηματικά και στους Ηλεκτρονικούς Υπολογιστές, ενώ στη συνέχεια σπούδασε νευροχειρουργός. Γνωρίζει Λατινικά, Γαλλικά, Ισπανικά και Γερμανικά και θέλει να μάθει Ρώσικα γιατί το Κυριλλικό αλφάβητο αποτελεί γι’ αυτόν μία νέα πρόκληση.
28. Edith Stern
Την ημέρα που γεννήθηκε η Edith Stern, ο πατέρας της είπε χαρακτηριστικά ότι θέλει να κάνει την κόρη του έναν τέλειο άνθρωπο. Σε ηλικία 5 ετών ο πατέρας της, την έβαλε να διαβάσει ολόκληρη την εγκυκλοπαίδεια Μπριτάνικα, μπήκε στο πανεπιστήμιο όταν ήταν 12 χρονών και στα 15 της δίδασκε μαθηματικά σε πανεπιστημιακό επίπεδο. Έχει IQ 203 και δουλεύει στην IBM από το 1970.
27. Kim Ung-Yong
Ξεκίνησε μαθήματα όταν ήταν 3 ετών και στα 4 μιλούσε ήδη 4 γλώσσες. Στα 8 του η Νasa τον κάλεσε στην Αμερική για να σπουδάσει. Το IQ κυμαίνεται από 200 έως 210. Στα 16 του χρόνια έφυγε από τη Νasa και γύρισε πίσω στη Ν. Κορέα όπου πήρε το διδακτορικό του.
26. Francis Galton
Ο Francis Galton ήταν ένας Άγγλος πολυμαθής, γνωστός για την έρευνά του στην ευγονική και την ανθρώπινη νοημοσύνη. Σπούδασε μαθηματικά στο Πανεπιστήμιο του Κέιμπριτζ και έδειχνε μεγάλο ενδιαφέρον στην ψυχολογία. Σύμφωνα με υπολογισμούς είχε IQ 200.
25. Marie Curie
Γεννημένη στην Πολωνία, είναι γνωστή για την έρευνα που έκανε πάνω στη ραδιενέργεια. Το IQ υπολογίζεται ανάμεσα στο 180- 200. Η Curie ήταν η πρώτη γυναίκα που κέρδισε Βραβείο Νόμπελ, και ο πρώτος άνθρωπος που κέρδισε δύο φορές, πρώτη στην Φυσική και ύστερα στην Χημεία, αλλά και η πρώτη γυναίκα που δίδαξε στη Σορβόνη.
24. Thomas Wolsey
Ο Thomas Wolsey ήταν ένας καρδινάλιος του 16ου αιώνα που εκτιμάται ότι είχε IQ 200.
23. Hugo Grotius
Έζησε τον 17ο αιώνα και είναι γνωστός για τη συμβολή του στη νομική επιστήμη. Εκτιμάται ότι είχε IQ 200.
22. Υπατία
Έζησε τον 4ο αιώνα π.Χ. και ήταν φιλόσοφος, μαθηματικός και αστρονόμος. Εκτιμάται ότι το IQ της ήταν περίπου 170 έως 210.
21. Terence Tao
Με το ψευδώνυμο ο «Μότσαρτ των μαθηματικών», ο Tao είναι ένα παιδί θαύμα που διδάσκει μαθηματικά στο πανεπιστήμιο UCLA. Το IQ του κυμαίνεται από 211 έως 230, ανάλογα τη μέτρηση. Έγινε μέλος της διδακτικής ομάδας του Πανεπιστημίου, αφού πήρε το διδακτορικό του από το Πρίνστον σε ηλικία 21 ετών και ήταν ήδη μόνιμος καθηγητής στα 24 του. Έχει γίνει γνωστός για τη συμβολή του στη θεωρία των αριθμών και την αρμονική ανάλυση.
20. John Stuart Mill
Ήταν ένας πολιτικός φιλόσοφος του 19ου αιώνα και μέλος του Βρετανικού Κοινοβουλίου. Εκτιμάται ότι το IQ του είναι ανάμεσα στο 180-200.
19. Christopher Hirata
Το παιδί θαύμα που έγινε αστροφυσικός έχει IQ 225 και έγινε διάσημος το 1996 όταν έγινε, σε ηλικία 13 ετών, ο νεότερος νικητής στη Διεθνή Ολυμπιάδα Φυσικής. Μέχρι να γίνει 16 ετών δούλευε για τη NASA και στα 22 του πήρε το διδακτορικό του από το Πανεπιστήμιο Πρίνστον. Διδάσκει Φυσική και Αστρονομία στο Κοινοτικό Πανεπιστήμιο του Οχάιο.
18. Emanuel Swedenborg
Εκτιμάται ότι είχε IQ 165 έως 210 και ήταν επιστήμονας και θεολόγος που έζησε τον 18ο αιώνα. Οι ιδέες τους αναγνωρίστηκαν μετά τον θάνατό του.
17. Ettore Majorana
Ο Ettore Majorana ήταν ένας θεωρητικός φυσικός με IQ ανάμεσα στο 183 και το 200. Έγινε καθηγητής στο Πανεπιστήμιο της Νάπολης, έναν χρόνο πριν εξαφανιστεί μυστηριωδώς. Το πτώμα του δεν βρέθηκε ποτέ.
16. Βολτέρος
Γεννήθηκε στο Παρίσι το 1694 και εκτιμάται ότι το IQ έφτανε περίπου το 200. Ήταν ένας από τους πιο σημαντικούς συγγραφείς και φιλοσόφους της Γαλλίας, γνωστός για τη σατυρική του ευφυΐα και το κριτικό του πνεύμα.
15. William Shakespeare
Γεννήθηκε το 1564 και μέχρι το 1597 είχε ήδη δημοσιεύσει 15 έργα. Το IQ πιστεύεται ότι ήταν περίπου 210.
14. Nikola Tesla
Γεννήθηκε ένα βράδυ του 1856 που είχε καταιγίδα και ανακάλυψε το πηνίο Τέσλα και τις μηχανές εναλλασσόμενου ρεύματος. Εκτιμάται ότι ο δείκτης νοημοσύνης του κυμαινόταν από 160 έως 310, σε διαφορετικές μετρήσεις.
13. Leonhard Euler
Ο Σουηδός μαθηματικός και φυσικός γεννήθηκε το 1707 και πέρασε το μεγαλύτερο μέρος της καριέρας του στην Αγία Πετρούπολη και στο Βερολίνο. Το IQ του ήταν περίπου 200.
12. Galileo Galilei
Ο Γαλιλαίος ήταν ένας Ιταλός φιλόσοφος, αστρονόμος και μαθηματικός που γεννήθηκε το 1564 και ανέπτυξε διάφορα επιστημονικά μοντέλα. Το IQ του εκτιμάται ότι ήταν περίπου 200.
11. Carl Gauss
Θεωρείται ο μεγαλύτερος Γερμανός μαθηματικός του 19ου αιώνα και ξεχώρισε ως παιδί θαύμα στη θεωρία των αριθμών, την άλγεβρα, τη στατιστική και την ανάλυση. Εκτιμάται ότι ο δείκτης νοημοσύνης του κυμαινόταν από 250 έως 300. Τα κείμενα που είχε γράψει σχετικά με τον ηλεκτρομαγνητισμό, αλλά αρνήθηκε να δημοσιεύσει οτιδήποτε δεν ήταν τέλειο.
10. Thomas Young
Γιατρός και φυσικός, γεννημένος στην Βρετανία, ο Young ξεχώρισε σε πολλούς επιστημονικούς τομείς. Εκτιμάται ότι ο δείκτης νοημοσύνης του κυμαινόταν από 185 έως 200.
9. William Sidis
Ο Sidis που ήταν και η έμπνευση για την ταινία «Good Will Hunting», ήταν ένα παιδί θαύμα που μπορούσε να διαβάζει τους New York Times και να δακτυλογραφεί από την ηλικία των 2 ετών, σε αγγλικά και γαλλικά, έγινε δεκτός στο Πανεπιστήμιο του Χάρβαρντ σε ηλικία 9 ετών, αλλά το πανεπιστήμιο δεν του επέτρεψε να παρακολουθήσει τα μαθήματα επειδή ήταν «συναισθηματικά ανώριμος». Εκτιμάται ότι ο δείκτης νοημοσύνης του κυμαινόταν από 200 έως 300.
8. Gottfried Leibniz
Συνέβαλε σημαντικά στην φιλοσοφία της γλώσσας και την αρχή της λογικής. Ο Γερμανός φιλόσοφος εκτιμάται ότι είχε IQ από 182 έως 205.
7. Nicolaus Copernicus
Ο Κοπέρνικος ήταν Πολωνός μαθηματικός και αστρονόμος που ανακάλυψε το ηλιοκεντρικό μοντέλο του σύμπαντος και εξέλιξε την θεωρία του κόσμου. Εκτιμάται ότι το IQ του ήταν από 160 έως 200.
6. Rudolf Clausius
Ο Γερμανός φυσικός και μαθηματικός είναι κυρίως γνωστός για τον δεύτερο νόμο της θερμοδυναμικής και είχε δείκτη νοημοσύνης 190 με 205.
5. James Maxwell
Ο μαθηματικός και φυσικός από τη Σκωτία είναι γνωστός για την θεωρία του κλασσικού ηλεκτρομαγνητισμού και είχε δείκτη νοημοσύνης που κυμαινόταν από 190 έως 205.
4. Isaac Newton
Γνωστός για το νόμο της βαρύτητας, ο Άγγλος μαθηματικός και φυσικός έφερε την επανάσταση στα επιστημονικά του πεδία τον 17ο αιώνα. Εκτιμάται ότι ο δείκτης νοημοσύνης τους ήταν περίπου 200.
3. Leonardo da Vinci
Ζωγράφος, γλύπτης, αρχιτέκτονας, μουσικός, μαθηματικός, μηχανικός, εφευρέτης, γεωλόγος, χαρτογράφος, βοτανολόγος και συγγραφέας ο Λεονάρντο Ντα Βίντσι είναι ίσως ο πιο ταλαντούχος άνθρωπος που έζησε ποτέ. Εκτιμάται ότι το IQ του ήταν από 180 έως 220.
2. Albert Einstein
Ο Άλμπερτ Αϊνστάιν γεννήθηκε στη Γερμανία και ήταν Γερμανός θεωρητικός φυσικός και φιλόσοφος της επιστήμης με δείκτη νοημοσύνης που κυμαίνεται από 205 έως 225.
1. Johann Goethe
Ο Αϊνστάιν τον θεωρούσε τον «τελευταίο άνθρωπο στη Γη που γνωρίζει τα πάντα«. Ο Goethe ήταν ένας Γερμανός πολυμαθής που ανέπτυξε μία από τις πιο σημαντικές θεωρίες της εξέλιξης. Εκτιμάται ότι ο δείκτης νοημοσύνης του κυμαινόταν από 210 έως 225. Επιπλέον, θεωρείται μία από τις πιο εμβληματικές φιγούρες της δυτικής λογοτεχνίας, γράφοντας το 1808 ένα από τα πιο σημαντικά βιβλία έως σήμερα, το «Φάουστ».
Πηγή: Business Insider
Ακολουθήστε το Cretanmagazine στο Google News και στο Facebook